Triton's make_block_ptr Explained: A Visual Guide

When writing code for GPUs, performance is all about memory. How fast can you get the right data from the GPU's large, slow memory into its small, lightning-fast compute units? In the world of Triton, the key to this puzzle is a function called tl.make_block_ptr.

This function doesn't actually load any data. Instead, it creates a smart "viewfinder" that tells a program exactly where and how to access a small tile of data from a large tensor. Let's break down how it works.

The Big Picture: Our Scenario

To make things concrete, we'll use one consistent example. Imagine we are working on a query tensor q from a Transformer model.

• Tensor Shape: Our q tensor has a shape of [B, T, HQ, K], which stands for:
  • B: Batch size (we'll use 1)
  • T: Sequence Length (e.g., 1024 tokens)
  • HQ (or H in multi-head attention): Number of Query Heads (e.g., 8 heads)
  • K: Dimensions per head (e.g., 64 dimensions)
• Our Goal: We want to load one tile of data from this tensor with a shape of [BT, BK] (row height and column width of the tiled matrix, respectively), for example, 128 tokens by 64 dimensions.

Before we use the pointer, we first need to understand how this [1, 1024, 8, 64] tensor actually lives in memory.

How Tensors Live in Memory: Strides

A multi-dimensional tensor is not a grid in memory; it's a single, flat, continuous line of numbers. Strides are the numbers that tell us how to navigate this line as if it were a grid. A stride for a dimension tells you how many spots to jump in the flat line to move one step in that dimension.

For our q tensor with shape (T=1024, HQ=8, K=64) (ignoring B=1), the strides are:

• Stride K: 1. To get to the next element in the innermost dimension, just move one spot.
• Stride HQ: K = 64. To get to the next head, you must skip all 64 elements of the current head.
• Stride T: HQ * K = 8 * 64 = 512. To get to the next token, you must skip all 8 heads associated with the current token, which is 512 elements.

With this foundation, we can now build our block pointer.

Deconstructing make_block_ptr

Here is the full function call we will dissect:

p_q = tl.make_block_ptr(
    base=q + (bos * HQ + i_hq) * K,
    shape=(T, K),
    strides=(HQ*K, 1),
    offsets=(i_t * BT, 0),
    block_shape=(BT, BK)
)

Let's go through it parameter by parameter.

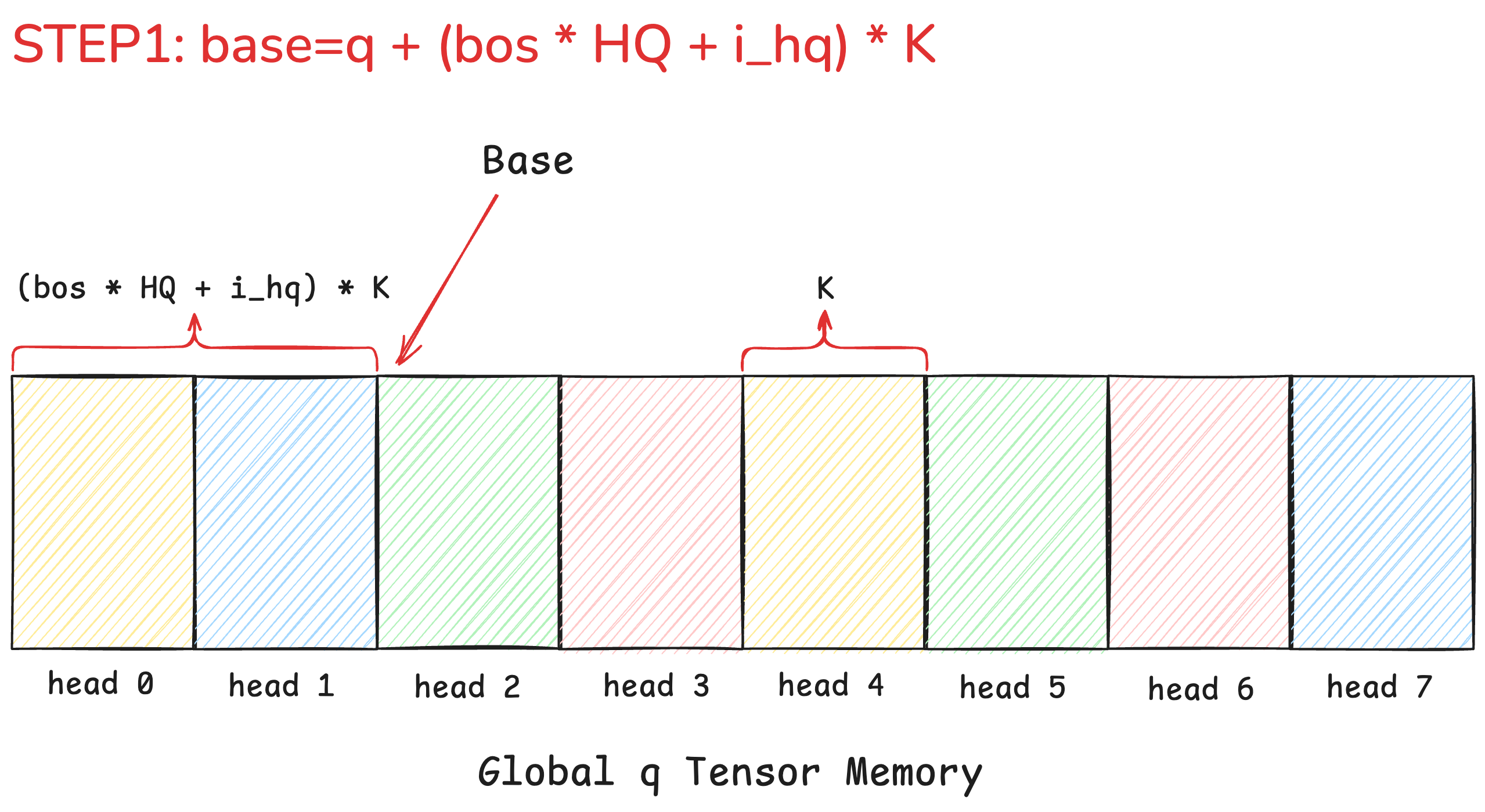
1. base=q + (bos * HQ + i_hq) * K

The base pointer's job is to find the very first memory address for the data slice we care about. In attention, we process one head at a time. So, the base calculation finds the starting point for a specific head (i_hq) within a specific sequence.

Let's break down the calculation q + (bos * HQ + i_hq) * K. The goal is to find the memory address of the first element q[i_b, 0, i_hq, 0]. The term (bos * HQ + i_hq) calculates the total number of heads we need to skip from the absolute beginning of the tensor. Here, it starts with bos (beginning of sequence), a variable used for varlen support (see FLA's attn code for more details) - in fixed length case, it is simply i_b * T. Together with i_hq, the expression is effectively counting the heads in all previous batches and time steps. We then multiply this total head count by K (the size of each head vector) to convert it into a memory offset. Adding this offset to q (the start of the tensor) gives us the precise starting address for our target head.

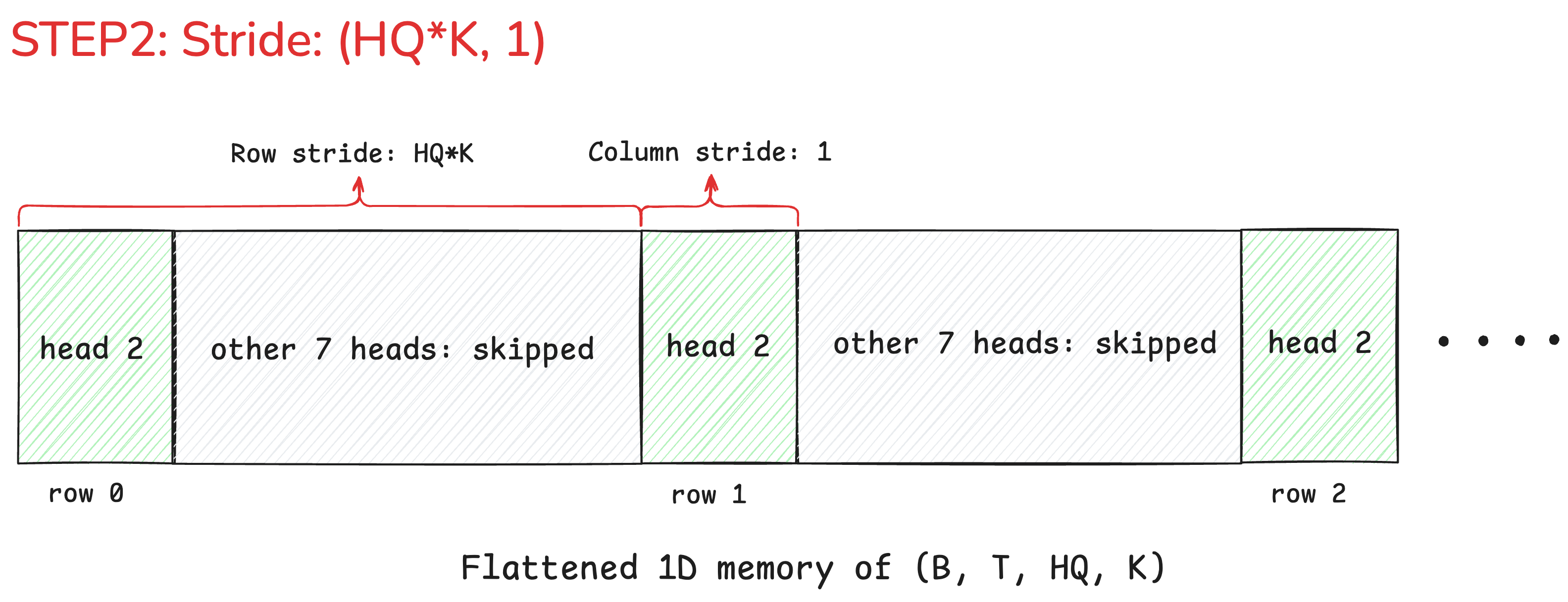
2. shape & strides

Once base gets us to the right neighborhood, shape and strides tell the pointer how to see the world from that point.

• shape=(T, K): We tell the pointer to logically view the data for this one head as a 2D grid of 1024 rows (tokens) and 64 columns (dimensions).
• strides=(HQ*K, 1): This is the crucial part. It connects our logical grid to the physical memory layout. It tells the pointer the rules for navigation: to move one column right, step 1 spot in memory. But to move one row down, you must make a giant leap of HQ * K = 512 spots.

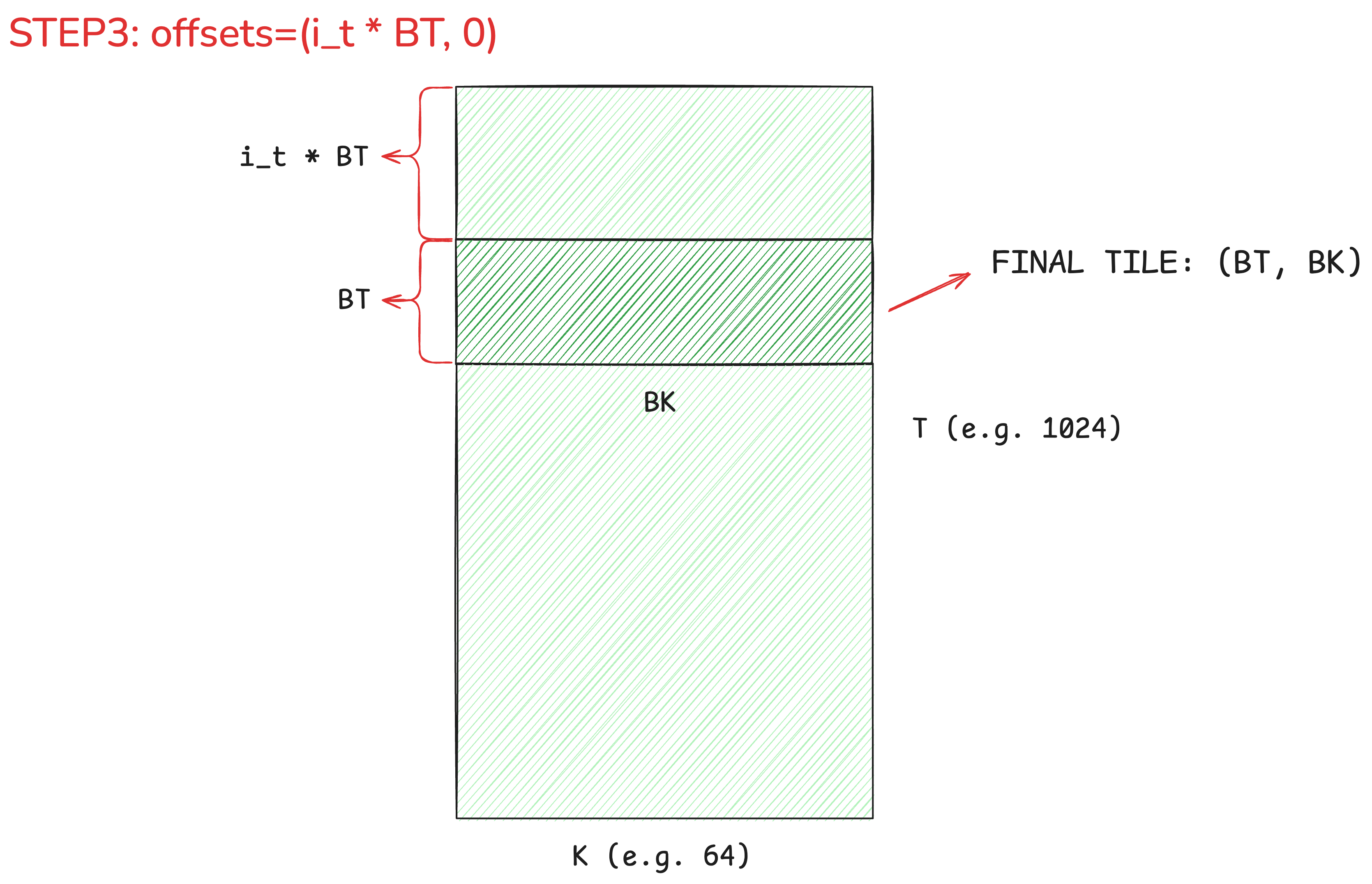
3. offsets & block_shape: Selecting the Tile

We have multiple programs running in parallel. Each needs to work on a different tile. That's where offsets comes in.

• offsets=(i_t * BT, 0): This tells the pointer to move its starting position from the base. A program responsible for the 3rd block of tokens (i_t=2) will offset its view by 2 * 128 = 256 rows down.
• block_shape=(BT, BK): Finally, this defines the size of the rectangle we actually want to grab. After applying the offset, the pointer knows to select a 128x64 block of data.

And that's it. Our p_q pointer is now fully configured. When we later call tl.load(p_q), Triton uses all this information to efficiently fetch the correct tile from global memory.

Bonus: The order Parameter and Virtual Transposes

If you have read through actual use cases of make_block_ptr, you might have noticed that it has one last parameter: order. This is a powerful optimization hint for the Triton compiler, and it's key to getting the best performance. Its goal is to achieve memory coalescing, where the GPU reads a whole chunk of adjacent memory in one go.

Let's look at how the key tensor k is handled in an attention kernel. Even though k is stored row-major just like q, it's often more efficient to view it as a transposed matrix. As we discussed, make_block_ptr can create this "virtual transpose" for free:

# A virtual transpose for the key tensor `k`
p_k = tl.make_block_ptr(
    ...,
    shape=(K, T),      # Note the swapped shape
    strides=(1, H*K),  # Note the swapped strides
    order=(0, 1)       # The special sauce!
)

For this "pretend" (K, T) shape, the data is physically contiguous down the K dimension (our new "rows"), since its stride is 1.

The order=(0, 1) parameter tells Triton: "Hey, for this pointer, prioritize dimension 0 for memory access." Since dimension 0 is the one with the stride of 1, Triton can schedule its threads to read a perfectly continuous block of memory, which is incredibly fast.

This reveals a simple rule of thumb:

• For a standard row-major view with strides=(..., 1), use order=(1, 0) to prioritize the columns.
• For a column-major view (or a virtual transpose) with strides=(1, ...) use order=(0, 1) to prioritize the rows.

By matching the order to the dimension with the stride of 1, you tell Triton exactly how to achieve the fastest possible memory access for any given tensor layout.