Overview

This is part one of the complete series on implementing Flash Attention in TileLang. This part focuses on the forward pass implementation.

The assumption is that readers already have an understanding about Flash Attention by e.g., knowing how block tiling and partial softmax work, and would like to learn more about its implementation. Tilelang is a high level GPU programming language - similar to Triton but much faster in some cases (like this one).

FlashAttention-2 is the established baseline, a CUDA kernel heavily optimized for NVIDIA's hardware architecture. Its performance comes from minimizing traffic to high-latency HBM (High-Bandwidth Memory) by maximizing computation within the fast, on-chip SRAM of each Streaming Multiprocessor (SM). Any attempt to outperform it must execute this strategy even more efficiently.

The following Tilelang implementation does exactly that. The kernel achieves >1.3x speedup over FlashAttention-2, reaching 630 TFLOPS/s for 4K sequence lengths on NVIDIA H100 GPUs.

Complete Kernel Code

@autotune(configs=get_configs())
@jit(out_idx=[-2, -1])
def mha_fwd(
    batch,
    seq_len,
    seq_len_kv,
    heads,
    dim,
    sm_scale,
    is_causal,
    block_M=128,
    block_N=128,
    num_stages=1,
    threads=256,
):
    sm_scale = (1.0 / dim)**0.5 * 1.44269504

    q_shape = [batch, heads, seq_len, dim]
    k_shape = [batch, heads, seq_len_kv, dim]
    v_shape = [batch, heads, seq_len_kv, dim]
    o_shape = [batch, heads, seq_len, dim]
    lse_shape = [batch, heads, seq_len]
    dtype = "bfloat16"
    accum_dtype = "float"
    q_start_id = seq_len_kv - seq_len

    @T.prim_func
    def main(
        Q: T.Tensor(q_shape, dtype),
        K: T.Tensor(k_shape, dtype),
        V: T.Tensor(v_shape, dtype),
        Output: T.Tensor(o_shape, dtype),
        Lse: T.Tensor(lse_shape, accum_dtype),
    ):
        with T.Kernel(T.ceildiv(seq_len, block_M), heads, batch, threads=threads) as (bx, by, bz):
            # Memory allocations
            Q_shared = T.alloc_shared([block_M, dim], dtype)
            K_shared = T.alloc_shared([block_N, dim], dtype)
            V_shared = T.alloc_shared([block_N, dim], dtype)
            O_shared = T.alloc_shared([block_M, dim], dtype)
            acc_s = T.alloc_fragment([block_M, block_N], accum_dtype)
            acc_s_cast = T.alloc_fragment([block_M, block_N], dtype)
            acc_o = T.alloc_fragment([block_M, dim], accum_dtype)
            scores_max = T.alloc_fragment([block_M], accum_dtype)
            scores_max_prev = T.alloc_fragment([block_M], accum_dtype)
            scores_scale = T.alloc_fragment([block_M], accum_dtype)
            scores_sum = T.alloc_fragment([block_M], accum_dtype)
            logsum = T.alloc_fragment([block_M], accum_dtype)

            # Load Q tile
            T.copy(Q[bz, by, bx * block_M:(bx + 1) * block_M, :], Q_shared)
            T.fill(acc_o, 0)
            T.fill(logsum, 0)
            T.fill(scores_max, -2**30)

            # Determine loop range with causal masking
            loop_range = (
                T.min(T.ceildiv(seq_len_kv, block_N),
                T.ceildiv(seq_len_kv - seq_len + (bx + 1) * block_M, block_N)
            ) if is_causal else T.ceildiv(seq_len_kv, block_N)

            # Main attention loop
            for k in T.Pipelined(loop_range, num_stages=num_stages):
                # Load K tile
                T.copy(K[bz, by, k * block_N:(k + 1) * block_N, :], K_shared)
                
                # Initialize scores with causal masking
                for i, j in T.Parallel(block_M, block_N):
                    q_idx = bx * block_M + i + q_start_id
                    k_idx = k * block_N + j
                    acc_s[i, j] = T.if_then_else(q_idx >= k_idx, 0, -T.infinity(acc_s.dtype))
                
                # Compute attention scores
                T.gemm(Q_shared, K_shared, acc_s, transpose_B=True, policy=T.GemmWarpPolicy.FullRow)

                # Softmax preparation
                T.copy(scores_max, scores_max_prev)
                T.reduce_max(acc_s, scores_max, dim=1, clear=False)
                for i in T.Parallel(block_M):
                    scores_scale[i] = T.exp2(scores_max_prev[i] * sm_scale - scores_max[i] * sm_scale)
                
                # Compute exp scores
                for i, j in T.Parallel(block_M, block_N):
                    acc_s[i, j] = T.exp2(acc_s[i, j] * sm_scale - scores_max[i] * sm_scale)
                T.reduce_sum(acc_s, scores_sum, dim=1)
                
                # Update running statistics
                for i in T.Parallel(block_M):
                    logsum[i] = logsum[i] * scores_scale[i] + scores_sum[i]
                T.copy(acc_s, acc_s_cast)
                for i, j in T.Parallel(block_M, dim):
                    acc_o[i, j] *= scores_scale[i]
                
                # Accumulate output
                T.copy(V[bz, by, k * block_N:(k + 1) * block_N, :], V_shared)
                T.gemm(acc_s_cast, V_shared, acc_o, policy=T.GemmWarpPolicy.FullRow)
            
            # Final normalization
            for i, j in T.Parallel(block_M, dim):
                acc_o[i, j] /= logsum[i]
            T.copy(acc_o, O_shared)
            T.copy(O_shared, Output[bz, by, bx * block_M:(bx + 1) * block_M, :])
            
            # Save logsumexp
            for i in T.Parallel(block_M):
                logsum[i] = T.log2(logsum[i]) + scores_max[i] * sm_scale
            T.copy(logsum, Lse[bz, by, bx * block_M:(bx + 1) * block_M])

    return main

Kernel design

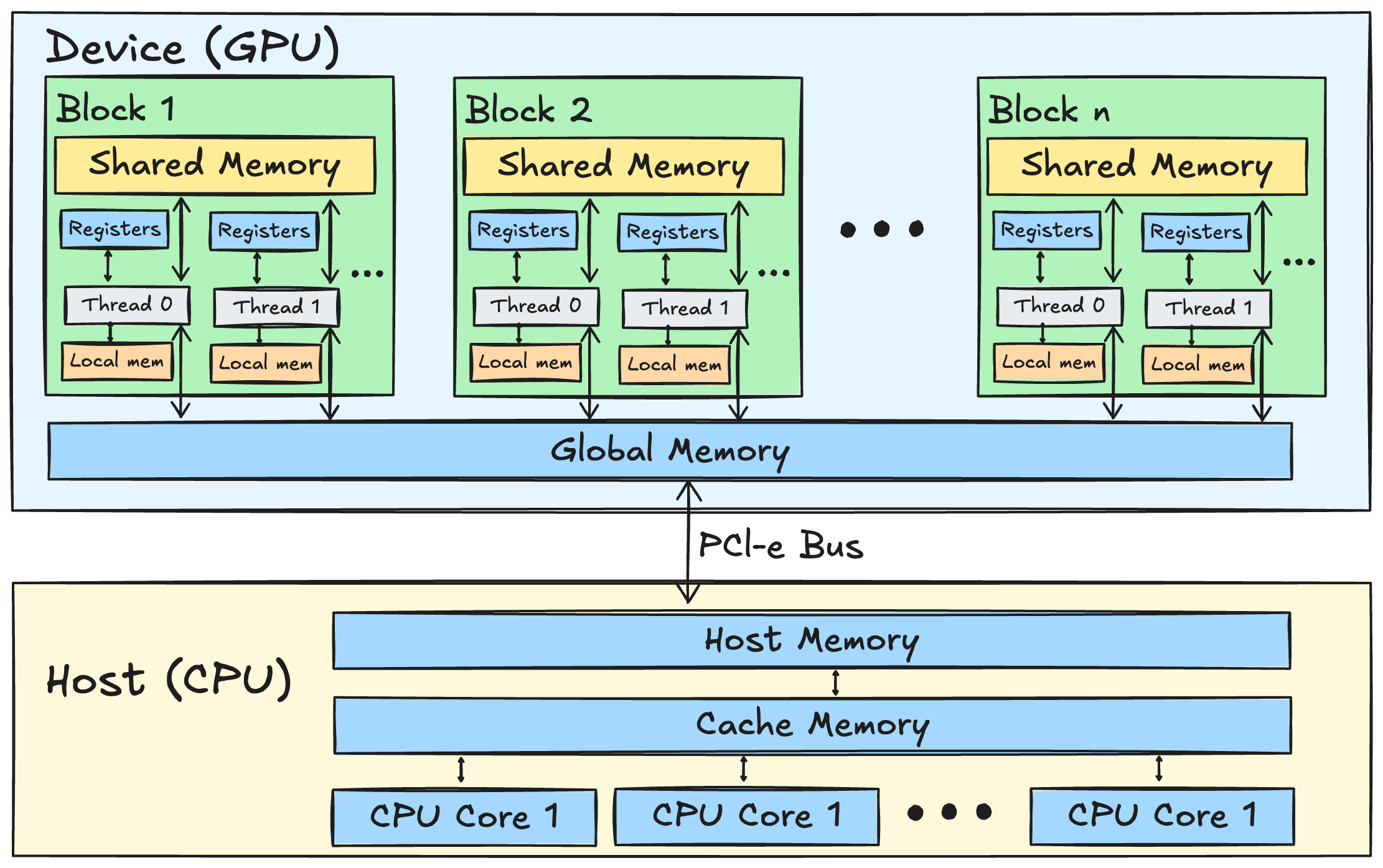
A block diagram of a CPU-GPU computing model. The GPU's architecture includes register, local, shared, and global memories, while the CPU operates with cache and host memory, enhancing data access speeds at different levels.

The kernel's design maps directly to the GPU's hierarchy. The work is launched as a grid of thread blocks, where each block computes a [block_M, dim] tile of the output O. This block is assigned to a single SM, which will execute its instructions.

with T.Kernel(T.ceildiv(seq_len, block_M), heads, batch, threads=threads) as (bx, by, bz):
    # ... kernel body

Inside the block, memory allocations target specific levels of the SM's memory subsystem. T.alloc_shared will reserve space in the SM's unified L1 cache/shared memory bank. This on-chip SRAM offers vastly higher bandwidth (~33 TB/s on H100, GPUs Go Brrr) and lower latency than the off-chip HBM (~3.35 TB/s). Tiles of Q, K, and V are explicitly copied here from HBM for fast access during computation.

Q_shared = T.alloc_shared([block_M, dim], dtype)
acc_o = T.alloc_fragment([block_M, dim], accum_dtype)

Even faster than shared memory is the GPU's register file. T.alloc_fragment maps directly to these registers, which are private to each thread and offer near-instant access for the arithmetic units. The most frequently accessed data—the output accumulator acc_o and the softmax statistics—are stored here to minimize latency within the core computational loop.

The main loop iterates over the key/value sequence, structured as a software pipeline to hide the latency of HBM memory access.

for k in T.Pipelined(loop_range, num_stages=num_stages):
    # Stage 1: Load next K tile from HBM to SRAM
    T.copy(K[bz, by, k * block_N:(k + 1) * block_N, :], K_shared)
    
    # Stage 2: Compute with current tiles already in SRAM/registers
    T.gemm(...)

The T.Pipelined construct allows the SM's warp schedulers to execute instructions from different stages of the loop concurrently. While one set of warps is stalled waiting for the T.copy from HBM to complete, other warps can execute arithmetic instructions (T.gemm) on data that is already available in SRAM. This overlapping of memory transfers and computation is critical for keeping the SM's execution units, especially Tensor Cores, saturated. This is conceptually identical to the num_stages parameter in a Triton kernel, which controls the depth of the software pipeline to better hide memory latency.

The matrix multiplications are handled by T.gemm. This primitive is compiled to use the H100's fourth-generation Tensor Cores, which are specialized hardware units designed for high-throughput matrix multiply-accumulate (MMA) operations.

The kernel's use of bfloat16 for input tensors and float for the accumulator (accum_dtype) directly matches the mixed-precision MMA instructions these cores are built for, ensuring maximum arithmetic throughput (why is arithmetic throughput important).

The T.GemmWarpPolicy further guides the compiler on how to arrange data within a warp's registers to perfectly align with the data input requirements of a hardware-level MMA instruction, eliminating unnecessary data movement. For example, a policy might dictate that each thread in a warp loads a specific row of a tile into its registers, creating the necessary layout for an efficient warp-wide matrix multiplication.

After the loop, the final output tile, which has been accumulated in the fast register file (acc_o), is normalized and written out to HBM only once.

You might notice the scaling factor sm_scale is multiplied by 1.44269504. This constant is the value of log_2​ of e. This is a common performance optimization that allows us to calculate the softmax using the faster hardware instruction exp2 instead of the standard exp. The rest of the kernel uses T.exp2 and T.log2 accordingly, ensuring the mathematical result is identical while maximizing speed.

Benchmarking

Here is the full benchmarking code in which the Tilelang kernel achieves over 1.3x speedup against Flash Attention 2:

import itertools
import functools
import torch
import tilelang
from tilelang import language as T
from tilelang import jit
from tilelang.autotuner import autotune
import torch.nn.functional as F

# Add flash attention 2 import
try:
    from flash_attn import flash_attn_func
    flash_attn_available = True
except ImportError:
    flash_attn_available = False
    print("flash-attn not available. Please install with: pip install flash-attn")

def print_red_warning(message):
    print(f"\033[31mWARNING: {message}\033[0m")

def calc_sim(x, y, name="tensor"):
    x, y = x.data.double(), y.data.double()
    denominator = (x * x + y * y).sum()
    if denominator == 0:
        print_red_warning(f'{name} all zero')
        return 1
    sim = 2 * (x * y).sum() / denominator
    return sim

def assert_similar(x, y, eps=1e-8, name="tensor", assert_=False, print_=True):
    sim = calc_sim(x, y, name)
    diff = 1. - sim
    if not (0 <= diff <= eps):
        print_red_warning(f'{name} Error: {diff}')
        if assert_:
            assert False
    else:
        if print_:
            print(f'passed: {name} diff={diff}')

def prepare_test_environment(seed=114514, cuda_device=3):
    torch.random.manual_seed(seed)
    torch.cuda.set_device(cuda_device)

def get_configs():
    iter_params = dict(
        block_M = [128,], block_N = [128,], num_stages = [1,], threads = [256,], # A100
        # block_M = [64, 128, 256],
        # block_N = [64, 128, 256],
        # num_stages = [1, 2, 3],
        # threads = [128, 256],
    )
    return [
        {k:v for k, v in zip(iter_params, values)}
        for values in itertools.product(*iter_params.values())
    ]

@autotune(configs=get_configs())
@jit(out_idx=[-2, -1])
def mha_fwd(
        batch,
        seq_len,
        seq_len_kv,
        heads,
        dim,
        tail_dim,
        sm_scale,
        is_causal,
        block_M=128,
        block_N=128,
        num_stages=1,
        threads=256,
):
    sm_scale = (1.0 / (dim + tail_dim))**0.5 * 1.44269504

    q_shape = [batch, heads, seq_len, dim + tail_dim]
    k_shape = [batch, heads, seq_len_kv, dim + tail_dim]
    v_shape = [batch, heads, seq_len_kv, dim]
    o_shape = [batch, heads, seq_len, dim]
    lse_shape = [batch, heads, seq_len]
    dtype = "bfloat16"
    accum_dtype = "float"
    q_start_id = seq_len_kv - seq_len

    @T.prim_func
    def main(
            Q: T.Tensor(q_shape, dtype), # type: ignore
            K: T.Tensor(k_shape, dtype), # type: ignore
            V: T.Tensor(v_shape, dtype), # type: ignore
            Output: T.Tensor(o_shape, dtype), # type: ignore
            Lse: T.Tensor(lse_shape, accum_dtype), # type: ignore
    ):
        with T.Kernel(T.ceildiv(seq_len, block_M), heads, batch, threads=threads) as (bx, by, bz):
            Q_shared = T.alloc_shared([block_M, dim], dtype)
            Q_tail_shared = T.alloc_shared([block_M, tail_dim], dtype)
            K_shared = T.alloc_shared([block_N, dim], dtype)
            K_tail_shared = T.alloc_shared([block_N, tail_dim], dtype)
            V_shared = T.alloc_shared([block_N, dim], dtype)
            O_shared = T.alloc_shared([block_M, dim], dtype)
            acc_s = T.alloc_fragment([block_M, block_N], accum_dtype)
            acc_s_cast = T.alloc_fragment([block_M, block_N], dtype)
            acc_o = T.alloc_fragment([block_M, dim], accum_dtype)
            scores_max = T.alloc_fragment([block_M], accum_dtype)
            scores_max_prev = T.alloc_fragment([block_M], accum_dtype)
            scores_scale = T.alloc_fragment([block_M], accum_dtype)
            scores_sum = T.alloc_fragment([block_M], accum_dtype)
            logsum = T.alloc_fragment([block_M], accum_dtype)

            T.copy(Q[bz, by, bx * block_M:(bx + 1) * block_M, :dim], Q_shared)
            if tail_dim > 0:
                T.copy(Q[bz, by, bx * block_M:(bx + 1) * block_M, dim:], Q_tail_shared)
            T.fill(acc_o, 0)
            T.fill(logsum, 0)
            T.fill(scores_max, -2**30)

            loop_range = (
                T.min(T.ceildiv(seq_len_kv, block_N), T.ceildiv(seq_len_kv - seq_len +
                    (bx + 1) * block_M, block_N)) if is_causal else T.ceildiv(seq_len_kv, block_N))

            for k in T.Pipelined(loop_range, num_stages=num_stages):
                # MMA0
                T.copy(K[bz, by, k * block_N:(k + 1) * block_N, :dim], K_shared)
                if tail_dim > 0:
                    T.copy(K[bz, by, k * block_N:(k + 1) * block_N, dim:], K_tail_shared)
                for i, j in T.Parallel(block_M, block_N):
                    q_idx = bx * block_M + i + q_start_id
                    k_idx = k * block_N + j
                    acc_s[i, j] = T.if_then_else(q_idx >= k_idx, 0, -T.infinity(acc_s.dtype))
                T.gemm(Q_shared, K_shared, acc_s, transpose_B=True, policy=T.GemmWarpPolicy.FullRow)
                if tail_dim > 0:
                    T.gemm(Q_tail_shared, K_tail_shared, acc_s, transpose_B=True, policy=T.GemmWarpPolicy.FullRow)
                # Softmax
                T.copy(scores_max, scores_max_prev)
                T.reduce_max(acc_s, scores_max, dim=1, clear=False)
                for i in T.Parallel(block_M):
                    scores_scale[i] = T.exp2(scores_max_prev[i] * sm_scale - scores_max[i] * sm_scale)

                for i, j in T.Parallel(block_M, block_N):
                    acc_s[i, j] = T.exp2(acc_s[i, j] * sm_scale - scores_max[i] * sm_scale)
                T.reduce_sum(acc_s, scores_sum, dim=1)
                for i in T.Parallel(block_M):
                    logsum[i] = logsum[i] * scores_scale[i] + scores_sum[i]
                T.copy(acc_s, acc_s_cast)
                for i, j in T.Parallel(block_M, dim):
                    acc_o[i, j] *= scores_scale[i]
                
                # MMA1
                T.copy(V[bz, by, k * block_N:(k + 1) * block_N, :], V_shared)
                T.gemm(acc_s_cast, V_shared, acc_o, policy=T.GemmWarpPolicy.FullRow)
            for i, j in T.Parallel(block_M, dim):
                acc_o[i, j] /= logsum[i]
            T.copy(acc_o, O_shared)
            T.copy(O_shared, Output[bz, by, bx * block_M:(bx + 1) * block_M, :])
            for i in T.Parallel(block_M):
                logsum[i] = T.log2(logsum[i]) + scores_max[i] * sm_scale
            T.copy(logsum, Lse[bz, by, bx * block_M:(bx + 1) * block_M])

    return main

def mha_fwd_interface(q, k, v, sm_scale, is_causal, return_kernel):
    assert q.is_contiguous() and k.is_contiguous() and v.is_contiguous()
    batch, heads, seq_len, dim_plus_tail_dim = q.shape
    _, _, seq_len_kv, dim = v.shape
    assert k.shape[:2] == v.shape[:2] == (batch, heads)
    assert k.shape[2:] == (seq_len_kv, dim_plus_tail_dim)
    tail_dim = dim_plus_tail_dim - dim

    kernel = mha_fwd(batch, seq_len, seq_len_kv, heads, dim, tail_dim, sm_scale, is_causal)
    if return_kernel:
        return kernel
    out, lse = kernel(q, k, v)
    return out, lse

def ref_mha_fwd_interface(q, k, v, sm_scale, is_causal):
    o_type, q, k, v = q.dtype, q.float(), k.float(), v.float()
    dim = q.size(-1)
    scores = torch.einsum('bhqd,bhkd->bhqk', q, k)
    sm_scale = dim ** -0.5 if sm_scale is None else sm_scale
    scores = scores * sm_scale
    if is_causal:
        seq_q = q.size(2)
        seq_kv = k.size(2)
        mask = torch.ones(seq_q, seq_kv, device=scores.device).tril(seq_kv-seq_q)
        mask = mask.unsqueeze(0).unsqueeze(0)
        scores = scores.masked_fill(mask == 0, float('-inf'))
    attention_weights = F.softmax(scores, dim=-1)
    output = torch.einsum('bhqk,bhkd->bhqd', attention_weights, v)
    lse = torch.logsumexp(scores, dim=-1)
    return output.to(o_type), lse

def check_prog(lib_outs, ref_outs, assert_=False, print_=True):
    tl_out, tl_lse = lib_outs
    ref_out, ref_lse = ref_outs
    assert_similar(tl_lse, ref_lse * 1.44269504, 1e-4, 'lse', assert_, print_)
    assert_similar(tl_out, ref_out, 1e-4, 'out', assert_, print_)

def fast_test():
    prepare_test_environment()
    B, S, SKV, H, DQK, DV, dtype = 1, 4096, 8192, 16, 128, 128, torch.bfloat16
    # B, S, SKV, H, DQK, DV, dtype = 1, 4096, 8192, 16, 192, 128, torch.bfloat16

    sm_scale, is_causal = None, True
    q = torch.randn((B, H, S, DQK), dtype=dtype, device='cuda')
    k = torch.randn((B, H, SKV, DQK), dtype=dtype, device='cuda')
    v = torch.randn((B, H, SKV, DV), dtype=dtype, device='cuda')

    check_prog(
         mha_fwd_interface(q, k, v, sm_scale=sm_scale, is_causal=is_causal, return_kernel=False),
         ref_mha_fwd_interface(q, k, v, sm_scale=sm_scale, is_causal=is_causal),
    )

def benchmark_flash_attn2(q, k, v, sm_scale, is_causal):
    """Benchmark Flash Attention 2 implementation"""
    if not flash_attn_available:
        print("Flash Attention 2 not available, skipping benchmark")
        return None
    
    # Flash attention expects (batch, seq_len, heads, dim) format
    # Current format is (batch, heads, seq_len, dim)
    q_fa = q.transpose(1, 2).contiguous()  # (B, S, H, D)
    k_fa = k.transpose(1, 2).contiguous()  # (B, SKV, H, D) 
    v_fa = v.transpose(1, 2).contiguous()  # (B, SKV, H, D)
    
    # Flash attention function
    def fa2_fn():
        return flash_attn_func(
            q_fa, k_fa, v_fa,
            dropout_p=0.0,
            softmax_scale=sm_scale,
            causal=is_causal
        )
    
    import triton
    ms = triton.testing.do_bench(fa2_fn, rep=100, warmup=250)
    return ms

def benchmark(autotune=False):
    prepare_test_environment()
    # Use same head dimension for fair comparison
    B, S, SKV, H, DIM, dtype = 1, 4096, 4096, 16, 128, torch.bfloat16
    DQK, DV = DIM, DIM  # Same dimension for Q, K, V

    sm_scale, is_causal = None, True
    q = torch.randn((B, H, S, DQK), dtype=dtype, device='cuda')
    k = torch.randn((B, H, SKV, DQK), dtype=dtype, device='cuda')
    v = torch.randn((B, H, SKV, DV), dtype=dtype, device='cuda')

    if autotune:
        raise NotImplementedError('autotune is deprecated: 只能用在不被@autotune和@jit装饰的老版函数上')
        supply_prog = lambda params: [q, k, v]
        def tune_kernel(block_M=None, block_N=None, num_stages=None, threads=None):
            return mha_fwd(B, S, SKV, H, DV, DQK-DV, sm_scale, is_causal, block_M, block_N, num_stages, threads)
        ref_out, ref_lse = ref_mha_fwd_interface(q, k, v, sm_scale=sm_scale, is_causal=is_causal)
        ref_prog = lambda *args, **kwargs: (ref_out, ref_lse)
        tunner = tilelang.autotuner.AutoTuner.from_kernel(configs=get_configs(),kernel=tune_kernel).set_compile_args(out_idx=[-2, -1]).set_profile_args(ref_prog=ref_prog, supply_prog=supply_prog, manual_check_prog=check_prog)
        best = tunner.run()
        latency = best.latency
        print(best.config)
        print(f'fwd latency = {latency:.3f} ms')
        # Use the 2-FLOP-per-MAC convention (multiply + add)
        print(f'fwd flops = ', (2 * B * H * S * SKV * (DQK + DV)) / (latency * 1e-3) / 1e12)
    else:
        # Benchmark TileLang implementation
        # Compile the TileLang kernel *once* outside of the benchmarking loop so that
        # the measured number only reflects execution latency (Flash-Attention has
        # a similar one-time compilation step that happens during warm-up).
        tl_kernel = mha_fwd_interface(q, k, v, sm_scale=sm_scale, is_causal=is_causal, return_kernel=True)

        # We benchmark calling the already-compiled kernel. This avoids repeatedly
        # invoking Python as well as the @jit wrapper (which would otherwise be
        # executed inside the timed region), resulting in a fair apples-to-apples
        # comparison with Flash-Attention 2.
        fn = lambda: tl_kernel(q, k, v)
        import triton
        ms_tilelang = triton.testing.do_bench(fn, rep=100, warmup=250)
        
        # 2 FLOPs per multiply-accumulate (MAC) – the standard convention in DL papers
        flops = (2 * B * H * S * SKV * (DQK + DV)) / 1e12
        
        print("=== TileLang Implementation ===")
        print(f'fwd latency = {ms_tilelang:.3f} ms')
        print(f'fwd TFLOPS = {flops / (ms_tilelang * 1e-3):.2f}')
        print(f'Dimensions: Q/K/V={DIM}')
        
        # Benchmark Flash Attention 2
        ms_fa2 = benchmark_flash_attn2(q, k, v, sm_scale, is_causal)
        if ms_fa2 is not None:
            print("\n=== Flash Attention 2 ===")
            print(f'fwd latency = {ms_fa2:.3f} ms')
            print(f'fwd TFLOPS = {flops / (ms_fa2 * 1e-3):.2f}')
            print(f'Dimensions: Q/K/V={DIM}')
            
            # Speedup comparison
            speedup = ms_fa2 / ms_tilelang
            print(f"\n=== Comparison ===")
            print(f'TileLang vs Flash Attention 2 speedup: {speedup:.2f}x')
            if speedup > 1:
                print(f'TileLang is {speedup:.2f}x faster than Flash Attention 2')
            else:
                print(f'Flash Attention 2 is {1/speedup:.2f}x faster than TileLang')
            
            print(f"\nBoth implementations process the same problem size: {DIM} head dimensions")
            print(f'Total FLOPS: {flops:.2f} TFLOPS')

if __name__ == "__main__":
    fast_test()
    benchmark()